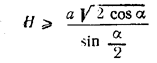Правильную четырехугольную призму требуется пересечь плоскостью так, чтобы в сечении получился ромб с острым углом α. Найти угол наклона секущей плоскости к основанию.

Четырехугольник AMKN (рис.), получающийся в сечения боковой поверхности призмы, всегда является параллелoграммом (доказать!).

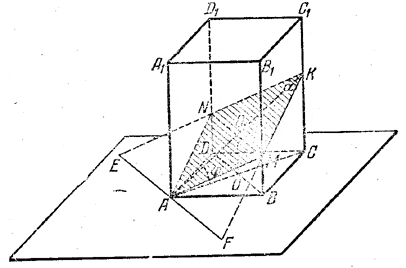
Чтобы он был ромбом, должно быть AM=AN. Из равенства треугольников ADN и АВМ (доказать!) следует, что DN = BM. Значит, прямая МN параллельна прямой BD, а значит, и плоскости ABCD. Следовательно, прямая EF, по которой плоскость AMKN пересекается с плоскостью ABCD, параллельна диагонали MN (и диагонали BD), а значит, перпендикулярна другой диагонали ромба АК (и диагонали АС).

Отсюда следует, что φ = ∠CAK есть линейный угол искомого двугранного угла. Прямая OO₁, соединяющая центр ромба О₁ с центром основания призмы, перпендикулярна к основанию (доказать!). Из треугольника AOO₁ находим

Замечание. Плоскость, проведенная через прямые AM и AN, пересечет ребро СС₁ лишь в том случае, если СС₁ > СК, т. е если высота призмы не меньше, чем

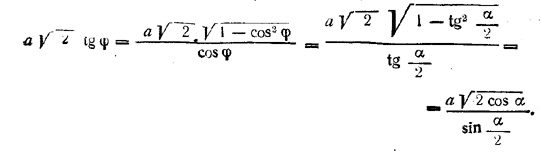
В противном случае ни через точку Ф, ни тем более через другую точку ребра АА₁ требуемого сечения провести нельзя.

Отв φ = arc cos tg ^α/₂.

Задача имеет решение только при условии