Основанием прямого параллелепипеда служит ромб с острым углом α. Под каким углом к основанию нужно пересечь этот параллелепипед плоскостью, чтобы в сечении получился квадрат с вершинами на боковых ребрах?
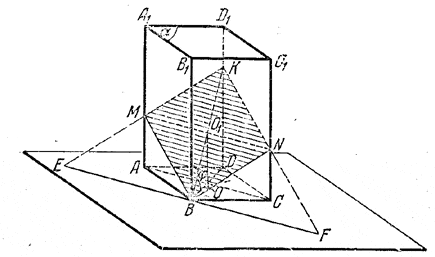
Так как MN = AC (рис.) и BK > BD, а по условию должно быть BK = MN, то AC>BD, т.е. ФС есть большая диагональ ромба, так что ∠ABC - тупой, a ∠BAD - острый.
Угол φ = ∠ОВО1 - линейный угол искомого двугранного угла.
Из треугольника ОО1В имеем ![]() , где ОВ = ОА • tg α/2.
, где ОВ = ОА • tg α/2.
А так как ОА = О1М = О1В, то 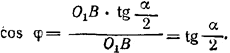 .
.
Здесь tg α/2< 1 , так как α - острый угол.
Ответ: φ = arc cos tg α/2.; задача имеет решение только при условии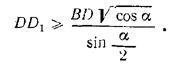
Похожие примеры: