Сторона основания правильной треугольной пирамиды равна а. Сечение, делящее угол между боковыми гранями пополам, есть прямоугольный треугольник. Определить объем пирамиды и угол между боковой гранью ее и плоскостью основания.
Чтобы провести сечение, делящее пополам двугранный, угол при ребре AD (рис.), нужно иметь линейный угол этого двугранного угла.
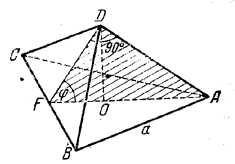
Таковым является угол BDC, так как плоскость BDC перпендикулярна к ребру AD. Действительно, во всякой правильной пирамиде боковое ребро AD перпендикулярно к противоположной стороне ВС основания (доказывается так же, как в в предыдущей задаче); кроме того, в данном случае ребра AD перпендикулярно также и к прямой FD. Действительно, по условию треугольник AFD - прямоугольный, а так как его углы при вершинах А и F непременно острые, то прямой угол есть ∠ ADF.
Так как OF = 1/2 OA = 1/2 R, тo
OD = √OF • ОА = R/√2 (где R = a/√3 ) Угол φ = ∠ AFD измеряет угол наклона грани BCD к плоскости основания. Имеем
tg φ = OD/OF = R/√2 : R/2 = √2
3амечание. Боковое ребро AD образует с ребром BD (и с ребром CD) прямой угол; так как наша пирамида - правильная, то и ребра BD и DC образуют прямой угол.
![]()