Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3√2 .
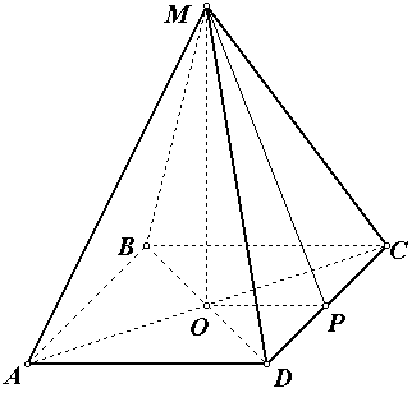
1) найдем сторону основания по формуле a = R√2, т.е. a = 3√2 * √2 = 6.
2) найдем периметр основания: Р = 4а, Р = 24.
3) из прямоугольного треугольника МDР по теореме Пифагора находим апофему МР: \( MP=\sqrt{MD^2 - DP^2}, DP = \frac{a}{2}\) тогда: \( МР = \sqrt{25-9}=\sqrt{16} = 4\).
4) вычислим площадь боковой поверхности пирамиды: \(S = \frac{1}{2}P\cdot h = \frac{1}{2} 24 \cdot 4 = 48 \).
Ответ: 48
Похожие примеры: