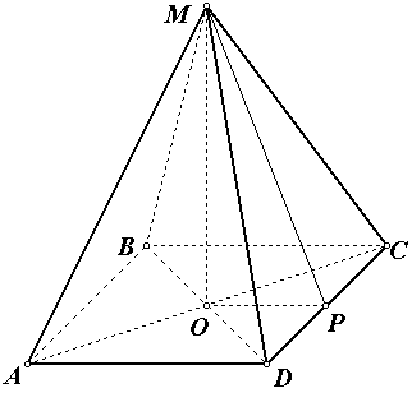
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.

2) по условию \(S=\frac{1}{2}P\cdot h=16\sqrt2\) т.е. \(\frac{1}{2}\cdot 8 \cdot h = 16\sqrt2 \Rightarrow h=4\sqrt2\)

3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: \(MO=\sqrt{MP^2 - OP^2}\), учитывая, что ОР =\( \frac{1}{2}a\)= 1, получаем: МО = \( \sqrt{(4\sqrt2)^2 - 1^2} = \sqrt{31}\).

Ответ: \( \sqrt{31}\)