$$ V=\frac{1}{3}S\cdot H $$

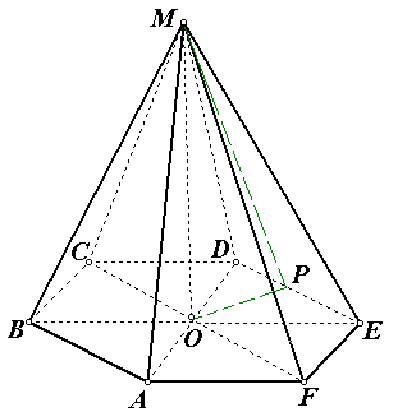
1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е. a = R, R = 4.

2) площадь правильного шестиугольника найдем по формуле \(S=6\cdot S_{\Delta}\) или \(S=\frac{3\sqrt3}{2}a^2 = 24\sqrt3\).

3) из прямоугольного треугольника МОВ найдем высоту МО: \(MO=\sqrt{BM^2 - BO^2}=\sqrt{25-16} =\sqrt9 =3\).

4) вычисляем объём пирамиды:\(V=\frac{1}{3}S\cdot H=\frac{1}{3} 24\sqrt3\cdot 3=24\sqrt3\).

Ответ: \(24\sqrt3\)