$$ V=\frac{1}{3}S\cdot H $$

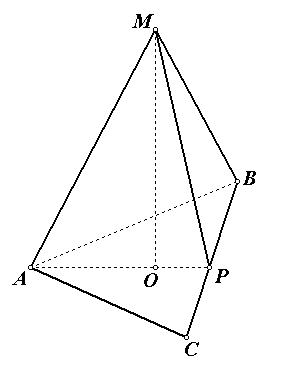
1) найдем сторону основания правильной пирамиды по формуле a = R√3, a = √3 · √3 = 3.

2) найдем площадь основания, как площадь правильного треугольника \(S=\frac{a^2\sqrt3}{4}, S=\frac{9\sqrt3}{4}\).

3) вычислим объём пирамиды:

$$ V=\frac{1}{3}S\cdot H, \;\; V=\frac{1}{3}\frac{9\sqrt3}{4}\cdot 4\sqrt3 = 9 $$