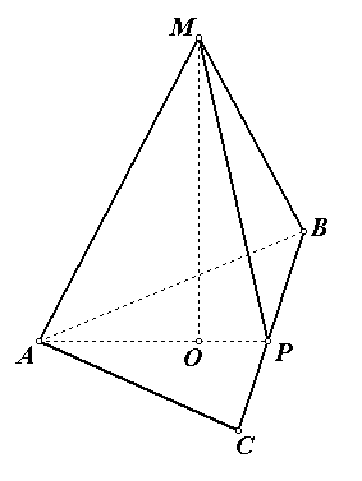
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. R = 2r, тогда R = 2 * 2 = 4.

2) найдем сторону основания правильной пирамиды по формуле a = R√3, a = 4√3

3) найдем площадь основания, как площадь правильного треугольника \(S=\frac{a^2 \cdot \sqrt3}{4}, S=\frac{(4\sqrt3)^2 \sqrt3}{4} = 12\sqrt3\).

4) вычислим объём правильной пирамиды: \( V =\frac{1}{3}S\cdot H = \frac{1}{3} 12 \sqrt3 3 \sqrt3 = 36\).

Ответ: 36