\(V=\frac{1}{3}S\cdot H \)

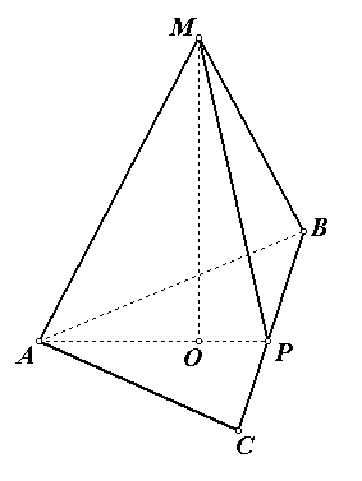
1) найдем радиус описанной около основания и вписанной в основание окружностей: \(a=R\sqrt3, R=\frac{a}{\sqrt3}, r=\frac{R}{2}\) то есть \( R=\frac{6}{\sqrt3}, r=\frac{3}{\sqrt3}\).

2) найдем площадь основания, как площадь правильного треугольника \(S=\frac{a^2 \cdot \sqrt3}{4}, S=\frac{36\sqrt3}{4}=9\sqrt3\).

3) из прямоугольного треугольника MOP по теореме Пифагора находим высоту: \(MO=\sqrt{MP^2 - OP^2}, MO = \sqrt{15-3}=\sqrt{12}=2\sqrt3\).

4) вычислим объём правильной пирамиды: \( V=\frac{1}{3}S\cdot H = \frac{1}{3}\cdot 9\sqrt3 \cdot 2\sqrt3 =18\).

Ответ. 18