\(V=\frac{1}{3}S\cdot H \)

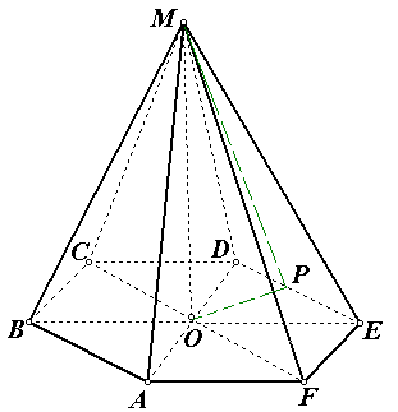
1) найдем площадь правильного шестиугольника по формуле \(S=6\cdot S_{\Delta}\) или \(S=\frac{3\sqrt3}{2}a^2 = 12\sqrt3\).

2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике a = R : \(MO=\sqrt{BM^2 - BO^2}=\sqrt{20-8} =\sqrt{12} =2\sqrt3\) .

3) вычисляем объём пирамиды: \(V=\frac{1}{3}S\cdot H=\frac{1}{3} 12\sqrt3\cdot 2\sqrt3=24 \).

Ответ: 24