Тетраэдр, ребро которого равно а, пересечен плоскостью, содержащей одно из ребер тетраэдра, и делящей противоположное ребро в отношении 2 : 1. Определить площадь сечения и углы этого сечения. (Под тетраэдром здесь понимается правильный четырехгранник (иногда тетраэдром называется произвольная треугольная пирамида).
По условию BE : EA = 2 : 1 (рис.).
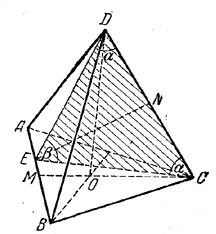
Сечение есть \(\Delta\)DEC. Haйдем его площадь S. Треугольник DEС - равнобедренный, так как EC=ED как соответственные стороны равных треугольников AЕС и AED (AC = AD; сторона AE - общая и ∠ CAE = ∠ DAE = 60°).
Проведем высоту его EN; тогда S = a • EN/2 Для определения EN найдем сначала ЕС из \(\Delta\)АСЕ (по теореме косинусов):
EС2 = AС2 + AE2 - 2 • AE • АС • cos 60° = 7/9 а2.
Теперь из \(\Delta\)ENC находим
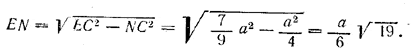
Обозначим углы сечения ∠ ECD = ∠ EDC через α. Тогда ∠ CED = π -2α. Из треугольника CEN имеем
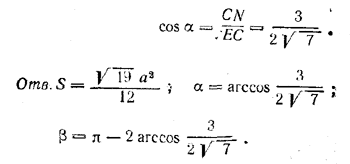
Похожие примеры: