Вычислить объем правильной пирамиды высоты h, зная, что в ее основании лежит многоугольник, сумма внутренних углов которого равна пπ, а отношение боковой поверхности пирамиды к площади основания равно k.
Так как сумма внутренних углов правильного многоугольника равна πn, то число сторон многоугольника равно п + 2.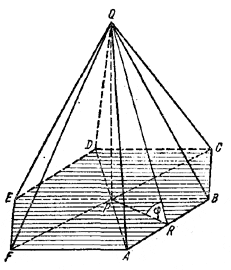
Пусть PQ-высота пирамиды. Рассмотрим какую-нибудь боковую грань пирамиды \(\Delta\)QAB и ее проекцию на основание, т. е. \(\Delta\)РAВ. Из условия задачи следует:
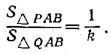
Так как площади данных треугольников относятся как их высоты, опущенные на общее основание АВ, то для косинуса двугранного угла при основании имеем:
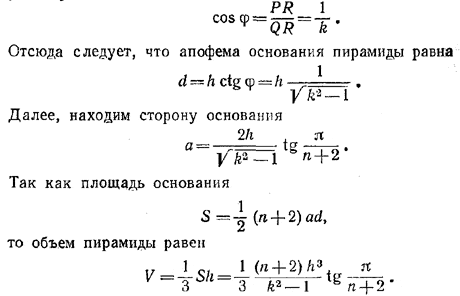
Похожие примеры: