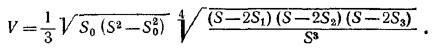Найти объем треугольной пирамиды, если площади ее граней равны S0, S1, S2, S3, а двугранные углы, прилежащие к грани с площадью S0, равны между собой.
Примем грань с площадью S0 за основание ABC данной пирамиды ABCD. Пусть DO - высота пирамиды, a DA1, DB1, DC1 - высоты боковых граней.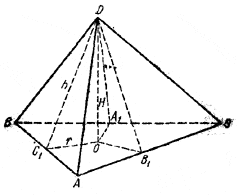
По теореме о трех перпендикулярах ОС1 ⊥ АВ, OA1 ⊥ BC и ОВ1 ⊥ АС, в силу чего углы ∠DC1O, ∠DA1O и ∠DB1O являются линейными углами соответствующих двугранных углов и по условию задачи равны. Отсюда следует равенство треугольников DОС1, DOA1 и DOB1. Для удобства вычислений введем следующие обозначения:
DO = H, DC1 = DA1 = DB1 = h, OC1 = OA1 = OB1 = r,
S1 +S2 + S3 = S.
Очевидно, что r есть радиус окружности, вписанной в \(\Delta\)ABC. Объем пирамиды ABCD равен
V=1/3S0H. (1)
Из прямоугольного треугольника DOC1 получим:
Н =√h2- r2 . (2)
Таким образом, задача сводится к нахождению апофемы h и радиуса r.
Из формулы S3 = 1/2ABh и ей аналогичных найдем выражения для сторон треугольника ABC:
![]()
Следовательно, полупериметр будет
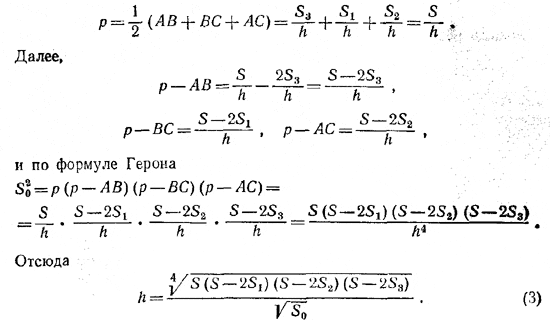
Радиус r вписанной окружности найдем из формулы, выражающей площадь S0 треугольника ABC через этот радиус и полупериметр:

Подставив это значение в формулу (2), получим:
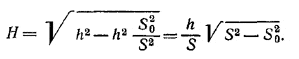
Подставив сюда значение h из равенства (3) и внеся полученный результат в формулу (1), окончательно получим: