Правильная треугольная пирамида пересечена плоскостью, проходящей через вершину основания и середины двух боковых ребер. Найти отношение боковой поверхности пирамиды к площади основания, если известно, что секущая плоскость перпендикулярна к боковой грани.
Пусть E и F - середины ребер правильной треугольной пирамиды SABC, D - середина отрезка EF.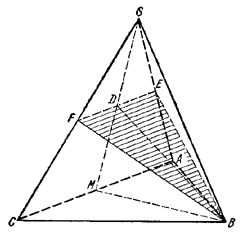
Так как сечение перпендикулярно грани CSA, то ∠SDB - прямой. Продолжив SD до пересечения с прямой АС в точке М, рассмотрим треугольник MBS. Точка D, очевидно, делит отрезок SM пополам. Так как, кроме того, BD⊥MS, то треугольник МBS равнобедренный; SB = MB.
Пусть сторона основания пирамиды равна а. Тогда
![]()
Высота боковой грани
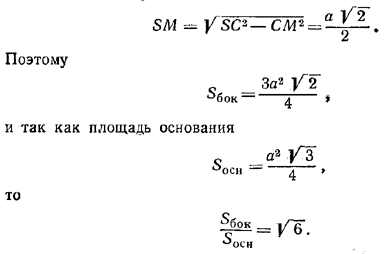
Похожие примеры: