Правильная пятиугольная пирамида SABCDE пересечена плоскостью, проходящей через вершины А и С основания и середины ребер DS и ES. Найти площадь сечения, если q есть длина стороны основания пирамиды, a b — длина бокового ребра.

Пусть М и N-середины ребер ES и DS;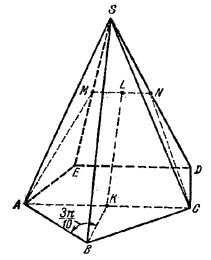

легко видеть, что AMNC-трапеция, ибо MN || ED, a ED || AC. Очевидно также, что

MN = ¹/₂ q

Используя формулу (1) для квадрата медианы треугольника в решении задачи 165, найдем:

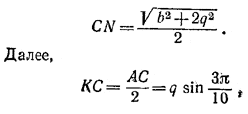
ибо ∠АВК = ^3π/₁₀. Если KL-отрезок, соединяющий середины оснований трапеции ACNM, то

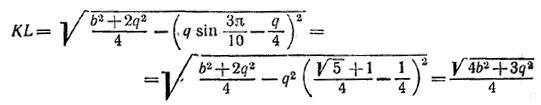
( мы воспользовались здесь тем, что ). Таким образом, искомая площадь

S_сеч. = ¹/₂ (MN + AC) KL = ^q/₁₆ (2 + √5) √4b²+3q²