Доказать, что разность между суммой квадратов расстояний произвольной точки М плоскости до двух противоположных вершин параллелограмма ABCD и суммой квадратов расстояний от той же точки до двух других вершин есть величина постоянная.

В обозначениях рис. 83 имеем:

МА² = МO² + АO² — 2МO • АО cos α,

МС² = МО² + СО² + 2МО • СО cos α.

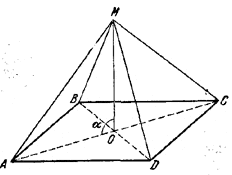
Pис. 83

Так как AО = СО, то, сложив эти равенства, получим;

МА² + МС²= 2МО² + 2АO². (1)

Аналогично

MB² + MD² = 2MO² + 2BO².

Следовательно, разность

(МА² + МС²) — (МВ² + MD²) = 2(AО² — ВО²)

не зависит от положения точки М.