Два треугольника ABC и А1В1С1 расположены симметрично друг другу относительно центра их общего вписанного круга радиуса r . Доказать, что произведение площадей ABC, А1В1С1 и шести треугольников, получившихся при пересечении сторон \(\Delta\)ABC и \(\Delta\)А1В1С1, равно r 16.
Симметрия в расположении ABC и A1B1C1 относительно центра вписанного круга О означает, что соответствующие точки \(\Delta\)ABC и \(\Delta\)А1В1С1 лежат на одной прямой с О и находятся на равном расстоянии от О.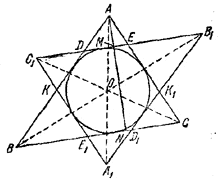
В частности, ОС = ОС1, ОВ = ОВ1 и ВСВ1С1 — параллелограмм; значит, ВС = В1С1. Аналогично АС = А1С1, АВ = A1B1 и \(\Delta\)ABC= \(\Delta\)А1В1С1.
Рассматривая параллелограммы АВА1В1, BDB1D1, ACA1C1 и ECE1C1, находим, что AD = A1D1, АЕ = А1Е1, а так как ∠A = ∠А1 то \(\Delta\)ADE = \(\Delta\)A1D1E1.
Аналогично \(\Delta\)B1EK1 = \(\Delta\)BE1K и \(\Delta\)DС1K = \(\Delta\)D1СK1
Введем обозначения:
S — площадь \(\Delta\)ABC,
S1 — площадь \(\Delta\)ADE,
S2 — площадь \(\Delta\)DC1K,
S3 — площадь \(\Delta\)KВЕ1,
АВ = с, ВС = а, АС = b,
hA, hB, hC — высоты, опущенные из вершин А, В, С. Тогда
![]()
Пусть AM — высота в \(\Delta\)ADE, AN — высота в \(\Delta\)ABC; тогда
![]()
Из подобия треугольников ABC и ADE находим:
![]()
Следовательно,
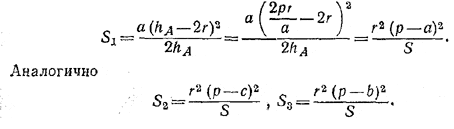
Используя формулу Герона, получаем:
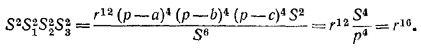
Похожие примеры: