Данный треугольник ABC пересечь прямой DE, параллельной ВС, так, чтобы площадь треугольника BDE равнялась заданной величине k². При каком соотношении между k²и площадью треугольника ABC задача разрешима и сколько она имеет решений?

Обозначим через S площадь данного треугольника ABC (рис.) и положим ^AD/_AB =x

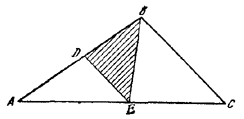
Рис.12

Тогда площадь \(\Delta\)ADE будет равна x²S, а площадь \(\Delta\)ABE равна xS. Условие задачи приводит к уравнению

xS — x²S= k²,

решив которое, получим:

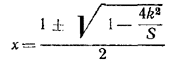
Задача разрешима, если S > 4k², и имеет два или одно решение в зависимости от того, будет ли S > 4k² или S = 4k²соответственно.