Через некоторую точку, взятую внутри треугольника, проведены три прямые, соответственно параллельные его сторонам. Эти прямые разделяют площадь треугольника на шесть частей, три из которых - треугольники с площадями, равными S₁, S₂, S₃. Найти площадь данного треугольника.

Обозначим через S площадь данного треугольника ABC. Полученные указанным в условии задачи построением треугольники с площадями S₁, S₂, S₃ подобны \(\Delta\)ABC (рис.).

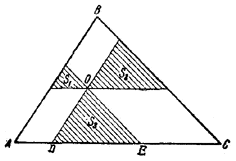
Поэтому их площади относятся как квадраты сходственных сторон, откуда

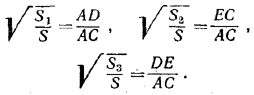
Сложив эти равенства почленно, найдем:

S = ( √S₁ + √S₂ + √S₃ )²