Даны стороны b и с треугольника. Найти третью сторону х, зная, что она равна опущенной на нeе высоте. При каком соотношении между b и с треугольник существует?

Третью сторону треугольника, равную опущенной на нее высоте, обозначим через х. Используя два выражения для площади данного треугольника, получим уравнение

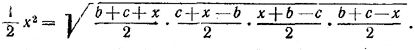
Решив его, найдем:

(1)

Необходимым условием разрешимости задачи является условие

3b²c² >b⁴ + с⁴. (2)

Если оно выполнено, то оба значения х² в (1) положительны. Легко проверить, что при выполнении (2) будут также выполнены неравенства

b + с > х > |b — с | ,

причем знак равенства имеет место только в том случае, когда x = 0. Последнее имеет место, если в (1) при b = с взять перед корнем знак минус. Следовательно, в случае b = с задача имеет единственное решение

Если b \(\ne\) с, то треугольник существует лишь в том случае, когда выполнено неравенство (2). Решив его относительно ^b/_c, найдем, что оно эквивалентно следующим неравенствам:

(3)

Следовательно, при b \(\ne\) с существуют два треугольника, если оба неравенства (3) выполнены со знаком <, и один треугольник, если хотя бы одно из неравенств (3) выполнено со знаком =.