Доказать, что сумма произведений высот остроугольного треугольника на отрезки их от ортоцентра до вершины равна полусумме квадратов сторон. Обобщить это предложение на случай тупоугольного треугольника.

Пусть ABC — остроугольный треугольник и AD, BE, CF — его высоты, пересекающиеся в точке О.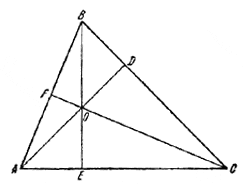

Каждый из четырехугольников BDOF, CEOD, AFOE является вписанным в некоторую окружность. По теореме о произведении секущей на ее внешнюю часть имеем:

AD•AO =AB•AF = AC•AE,

BE•BO = BC•BD = BA•BF,

CF•CO = CA•CE = CB•CD.

Сложив эти равенства, получим:

2 (AD•AO + BE•BO + CF•CO) =

= АВ•AF + BC•BD + CA•CE + AC•AE + BA•BF + CB•CD =

= АВ (AF + BF) + BC (BD + CD) + CA (СЕ + АЕ) =

= (АВ)² + (ВС)² + (СА)²,

что и требовалось доказать. В случае тупоугольного треугольника, произведение, соответствующее тупому углу, надо взять со знаком минус.