Треугольник АОВ повернут в своей плоскости вокруг вершины О на 90°, причем вершина А перешла в А₁, а вершина В — в В₁. Доказать, что в треугольнике OAB₁ медиана стороны AB₁ является высотой для \(\Delta\)OA₁В (аналогично медиана стороны А₁В в \(\Delta\)OA₁В является высотой для \(\Delta\)OAB₁).

Пусть ОС — медиана в \(\Delta\)OAB₁ . Пусть точка D лежит на продолжении ОС, причем ОС = CD.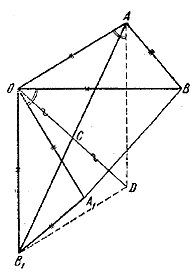

Покажем, что \(\Delta\)AОD = \(\Delta\)ОА₁В. Действительно, AO = OA₁ по построению. Далее, AOB₁D — параллелограмм, в силу чего AD = OB₁ = OB. Наконец ∠OAD = ∠А₁ОВ, так как стороны этих углов взаимно перпендикулярны: АО ⊥ OA₁ и OB₁ ⊥ OB по построению, a AD || OB₁
Следовательно, \(\Delta\)AOD = \(\Delta\)ОA₁В и две из сторон одного из них перпендикулярны, соответственно, двум сторонам другого. Поэтому третьи стороны также перпендикулярны, т. е. OD ⊥ A₁B.