Доказать, что если между сторонами a, b, с треугольника существует зависимость a² = b² + bc , то углы А и В, противолежащие сторонам а и b, удовлетворяют равенству ∠А = 2 ∠В.

Пусть дан \(\Delta\)ABC.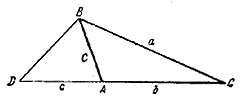

На продолжении стороны АС отложим AD = c. Из равенства a² = b² + bc следует:

Это означает, что треугольники CAB и CBD подобны и ∠А = ∠CBD. Кроме того, ∠В = ∠BDA = ∠DBA.

Следовательно, ∠A = ∠B + ∠DBA = 2 ∠В.