В равнобедренном треугольнике ABC угол при вершине В равен 20°. На боковых сторонах AB и BC взяты, соответственно, точки Q и P так, что ∠ACQ = 60°, a ∠CAP = 50°. Доказать, что ∠APQ = 80°.

Первое решение. Пусть QQ' || АС и N — точка пересечения AQ' и QC.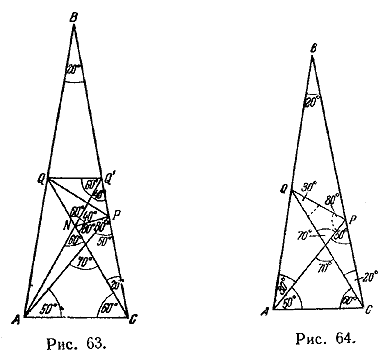

Сплошными дугами на рисунке обозначены углы, значения которых очевидны.

Покажем, что

QP ⊥ AQ'(1)

Действительно, NC = AC; но АС = РС, ибо \(\Delta\)АСР — равнобедренный. Поэтому NC = PC, следовательно, \(\Delta\)NCP также равнобедренный и значит

∠CNP = ∠NPC = 80°.

Отсюда уже легко получаем, что ∠Q'NP = 180° — 60° — 80° = 40°, и так как ∠NQ'P = 40°, то треугольники QQ'P и QNP равны.

Отсюда следует (1). Теперь уже ясно, что ∠Q'PQ = 50° и, следовательно,

∠QPA = 180° — 50° — 50° = 80°.

Второе решение (см. рис. 64).

Легко видеть, что угол Р =80° в том и только в том случае, если \(\Delta\)АВР ~ \(\Delta\)PCQ (сплошными дугами на рисунке отмечены углы, величины которых прямо следуют из условий задачи). Докажем, что эти треугольники действительно подобны. Для этого ввиду равенства углов АВР и PCQ достаточно проверить, что

^AB/_CQ= ^PB/_CP(1)

Положим АВ = l; тогда из равнобедренного треугольника CQB имеем:

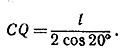
С другой стороны, так как РС=АС, то

PC = 2lsin 10°, а ВР = l — 2lsin 10°.

Подставив эти выражения в (1), придем к равносильному равенству:

4 sin 10° cos 20°= 1—2 sin 10°. (2)

Справедливость последнего легко обнаружить, заметив, что