Доказать, что угол треугольника будет острым, прямым или тупым, смотря по тому, будет ли противоположная сторона меньше, равна или больше удвоенной соответствующей медианы.

В треугольнике против большей стороны лежит больший угол. Поэтому, если в \(\Delta\)ABC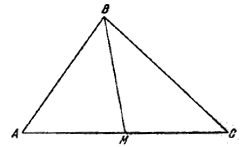

АС < 2 BM,

что равносильно двум неравенствам:

AM < BM, МС < BM,

то

∠ABM < ∠ВАМ, ∠MBC < ∠BCM.

Сложив эти неравенства, получим:

∠ABC < ∠ВАМ + ∠BCM = π - ∠ABC,

откуда 2 ∠ABC < π или ∠ABC < ^π/₂ .

Аналогично рассматриваются случаи АС > 2BM.