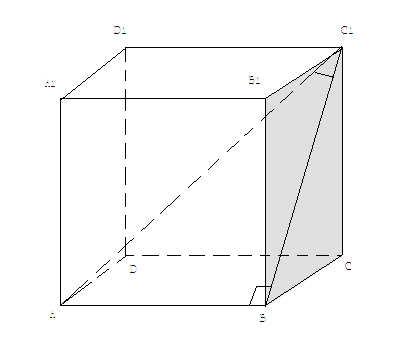
Из точки А опускаем перпендикуляр. Т.к. AB ⊥ BC, AB ⊥ BB₁, то AB ⊥ (BCC₁) и AB ⊥ BC₁ Тогда AC₁ – наклонная, ВС₁ – проекция прямой AC₁ на плоскость BСC₁. Т.к. угол между прямой и плоскостью – это угол между этой прямой и её проекцией на плоскость, то ∠AC₁B - искомый. Треугольник ABC₁ - прямоугольный. $$ tg\phi = \frac{AB}{BC_1} $$ Пусть сторона куба равна a. Тогда \(BC_1 = a\sqrt{2} \). $$ tg\phi = \frac{a}{a\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt2}{2} $$ Ответ: \(\frac{\sqrt2}{2}\)