Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне АВ.

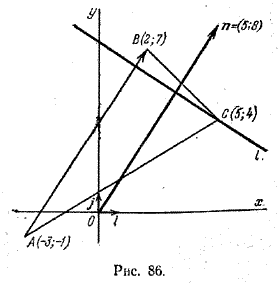
За нормальный вектор искомой прямой можно взять вектор n = \(\overrightarrow{AB}\).
Так как n = (2-(-3); 7 - (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

5(x- 5) + 8(y - 4) = 0,

или, окончательно, 5х + 8у - 57 = 0.