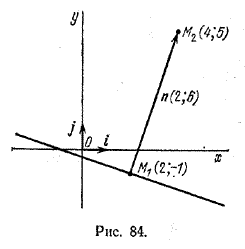
Даны точки М₁(2; -1) и М₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору \(\overrightarrow{M_{1}M_{2}}\).

Нормальный вектор искомой прямой n = \(\overrightarrow{M_{1}M_{2}}\) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле А(х — х₀) + В(у — у₀) = 0 получим уравнение

2(x-2) + 6(y+1) = 0

или х + 3y + 1 = 0.