В равнобедренном треугольнике с основанием а и боковой стороной b угол при вершине равен 20°. Доказать, что а³ + b ³ = 3аb².

Первое решение. Проведем АЕ так, чтобы ∠ЕАС = 20° и BD ⊥ АЕ (рис. 61).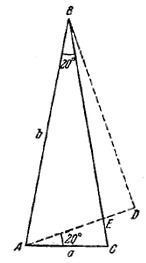

Так как \(\Delta\)САЕ ~\(\Delta\) ABC, то

^CE/_a = ^a/_b

откуда

С другой стороны, ∠BAD = 60°, в силу чего

BD =^√3/₂ b, AD = ^b/₂

и так как АЕ= а, то ED =^b/₂ — а.

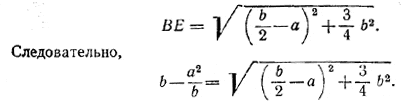
Возведя обе части в квадрат и сделав упрощения, найдем, что это соотношение равносильно доказываемому.

Второе решение. Так как a = 2b sin 10°, то доказываемое соотношение равносильно следующему:

1+8 sin³ 10° = 6 sin 10°,

или

sin 30°= 3 sin 10° — 4 sin³ 10°.

Последнее равенство выполнено в силу общей формулы

sin 3α = 3 sin α — 4 sin³ α.