Основанием пирамиды служит прямоугольник с острым углом α между диагоналями, а боковые ребра образуют с плоскостью основания угол φ. Определить объем этой пирамиды, если радиус шара, описанного около нее, равен R.

Плоскость основания пирамиды пересекает шар по кругу ABCD (рис.), описанному около основания.

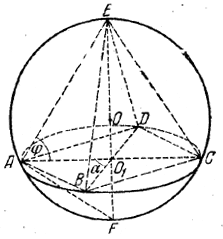
Высота пирамиды пройдет через центр О₁ этого круга (так как все ребра наклонены к основанию под равными углами), а также через центр О шара. Плоскость, проведенная через диагональ основания АС и вершину Е, пересечет шар по большому кругу, описанному около диагонального сечения пирамиды AЕС. Из \(\Delta\)АЕС, где угол AЕС равен 180°-2φ, находим по теореме синусов AC = 2R sin (180°-2φ) = 2R sin 2φ; значит, AO₁ = R sin 2φ. Из \(\Delta\)АЕО₁ найдем высоту пирамиды

ЕО₁ = H = AО₁ • tg φ = R sin 2φ tg φ.

Ответ: V = ²/₃ R³ sin³ 2φ sin α tg φ.