Радиус основания конуса равен R, а угол при вершине осевого сечения равен α. Найти объем правильной треугольной пирамиды, описанной вокруг конуса.

Так как радиус ОE (рис.) окружности, вписанной в основание, равен R, то AB = 2R√3 .

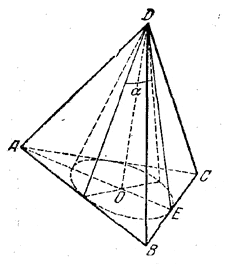
Из \(\Delta\)DOE находим DO = H = R ctg ^α/₂.

Ответ: V =√3 R³ctg ^α/₂ .