В конус вписан шар. Поверхность шара относится к площади основания конуса как 4:3. Найти угол при вершине конуса.

Пусть R - радиус основания конуса, α - угол между осью конуса и образующей, r - радиус вписанного шара. В осевом сечении конуса имеем равнобедренный треугольник ABC.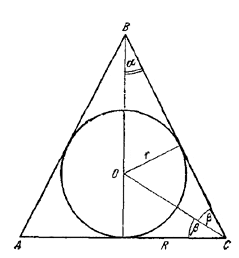

Радиус круга, вписанного в этот треугольник, равен радиусу r вписанного в конус шара. Пусть О - центр круга, ∠ОСА = β.

Тогда очевидно, что tg β = ^r/_R. Но по условию задачи

Отсюда ^r/_R = ¹/_√3 и, следовательно, β = ^π/₆. Так как, кроме того, α +2β = ^π/₂, то α= ^π/₆. Следовательно, искомый угол 2α = ^π/₃.