В конус вписана полусфера, большой круг которой лежит на основании конуса. Определить угол при вершине конуса, зная, что поверхность конуса относится к поверхности полусферы как 18:5.

Пусть r - радиус полусферы, R - радиус основания конуса, l - образующая конуса, α - угол между осью конуса и образующей.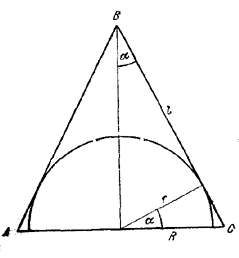

По условию задачи имеем

Введем в это равенство угол α. Для этого рассмотрим равнобедренный \(\Delta\)ABC, получающийся в осевом сечении конуса. Из \(\Delta\)ABC находим

R = l sin α, r = R cos α= l sin αcos α.

Подставляя эти выражения в левую часть (1), получаем

Так как cos²α = 1- sin²α, то, сократив дробь на 1+ sin α, будем иметь

36 sin²α- 36 sin α+ 5 = 0,

откуда

sin α₁ = ⁵/₆и sin α₂ = ¹/₆.

Следовательно, искомый угол при вершине конуса равен

2 arcsin ⁵/₆ или 2arcsin ¹/₆.