Конус и цилиндр имеют общее основание, а вершина конуса находится в центре другого основания цилиндра. Чему равен угол между осью конуса и его образующей, если известно, что полная поверхность цилиндра относится к полной поверхности конуса как 7:4.

Пусть α - искомый угол, l - образующая цилиндра, l₁ - образующая конуса, r - радиус оснований конуса и цилиндра.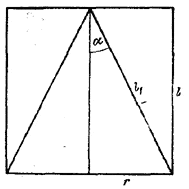

По условию

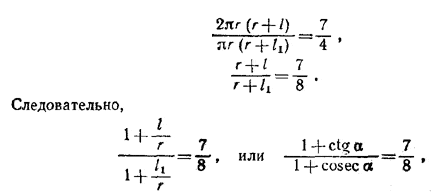
и, значит,

sin α+ 8 cos α-7 = 0.

Решив это уравнение, найдем:

sin α = ³/₅, α = arcsin ³/₅