В конус вписан цилиндр, высота которого равна радиусу основания конуса. Найти угол между осью конуса и его образующей, зная, что полная поверхность цилиндра относится к площади основания конуса как 3:2.

Пусть α - искомый угол, R - радиус основания конуса, r - радиус основания цилиндра.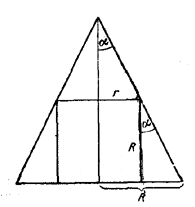

Имеем:

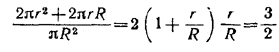
Но и, значит, ^r/_R = 1 - tg α. В результате получаем уравнение относительно tg α:

4tg² α- 12 tg α + 5 = 0.

Решив его, находим:

tg α= ⁵/₂или tg α= ¹/₂.

Легко видеть, однако, что , поэтому tg α= ¹/₂ и, следовательно,

α = arctg ¹/₂