В конус вписан цилиндр, высота которого равна радиусу основания конуса. Найти угол между осью конуса и его образующей, если полная поверхность цилиндра относится к площади основания конуса как 3 : 2.

Обозначим радиус OL цилиндра (рис.) через х, а радиус ОВ основания конуса через R.

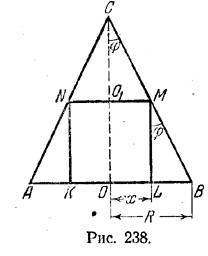
Так как по условию ML=R, то полная поверхность цилиндра S_п. =2πх² + 2πхR. По условию

2πх² + 2πхR = ³/₂πR² или х²+ Rx - ³/₄ R² = 0

откуда х = ^R/₂. (отрицательное решение х = - ³/₂R не годится). Из треугольника LMB находим

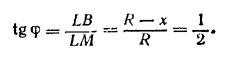
Ответ: φ = arctg ¹/₂.