Вычислить радиусы оснований усеченного конуса, описанного около шара радиуса R, зная, что отношение полной поверхности усеченного конуса к поверхности шара равно т.

Пусть S - полная поверхность конуса, S₁ - поверхность шара, r₁ и r - радиусы верхнего и нижнего оснований конуса, l - длина его образующей. Пусть далее CMDL-трапеция, полученная в осевом сечении конуса, О - центр вписанного шара, AB ⊥ LD и OF ⊥ MD.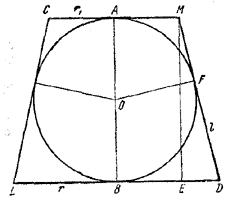

Имеем:

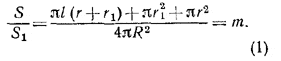
Легко видеть, что AM =MF и BD = FD, так как О - центр вписанного в трапецию круга, поэтому

l = r + r₁ (2)

Воспользовавшись этим равенством, из равенства (1) получим:

l² + r² + r₁² = 4mR². (3)

Из треугольника MED, далее, следует:

l² = ( r - r₁)² + 4R². (4)

Исключая l из равенств (2) и (4), найдем:

r r₁ = R². (5)

С помощью этого равенства, исключив l из (2) и (3), мы получим:

r² + r₁²= R²(2m-1). (6)

Решив теперь систему (5), (6), найдем:

r = ^R/₂( √2т + 1 + √2т -3);

r₁ = ^R/₂( √2т + 1 -√2т -3);

Таким образом, при т < ³/₂задача не имеет решения; при m = ³/₂ усеченный конус превращается в цилиндр.