Найти отношение объема шара к объему описанного около него прямого конуса, если полная поверхность конуса в n раз больше поверхности шара.

Пусть R - радиус шара, S_m и V_m - поверхность и объем шара, S_k и V_k - полная поверхность и объем конуса, h - высота конуса, r - радиус основания конуса.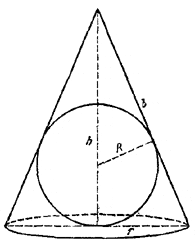

Тогда

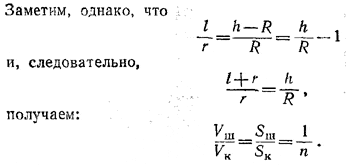
Замечание: К тому же результату можно прийти и более коротким путем, если воспользоваться следующей формулой:

V_k = ¹/₃S_kR (1)

где S_k - полная поверхность конуса, a R - радиус вписанного в него шара. Формула (1) легко получается из соответствующей формулы для пирамиды (см. решение задачи 240) предельным переходом. Действительно, так как, очевидно,

V_ш = ¹/₃S_шR, (2)

то, разделив (2) на (1), получим