В правильную n-угольную пирамиду со стороной основания а и боковым ребром b вписан шар. Найти его радиус.
Объем пирамиды равен сумме объемов пирамид, которые получатся, если соединить центр вписанного шара О со всеми вершинами пирамиды. Высота каждой такой пирамиды равна радиусу r шара, вписанного в данную пирамиду. Если S - площадь основания пирамиды, S1 - боковая поверхность, то объем пирамиды будетV= 1/3(S1 + S) r. (1)
Так как, с другой стороны,
V= 1/3 hS
то для rполучаем формулу
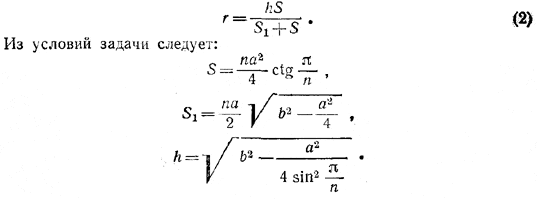
Подставляя эти выражения в (2), находим:
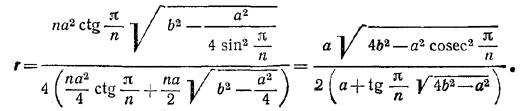
Похожие примеры: