Взяты две противоположные вершины куба и через середины шести ребер, не проходящих через эти вершины, проведена секущая плоскость, которая делит куб на две части. В каждую из этих частей помещен шар, касающийся трех граней куба и секущей плоскости. Во сколько раз объем каждого из этих шаров будет меньше объема куба?

Пусть A₁B₁C₁D₁E₁F₁ - правильный шестиугольник, полученный в сечении куба. Задача сводится к определению радиуса шара, вписанного в правильную шестиугольную пирамиду SA₁B₁C₁D₁E₁F₁.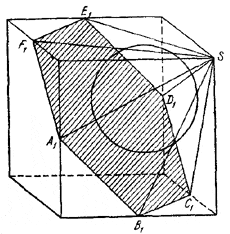

Сторона основания пирамиды равна ^a√2/₂ , а высота равна ^a√3/₂

Пользуясь тем, что радиус шара, вписанного в пирамиду, равен утроенному объему пирамиды, деленному на ее полную поверхность (см. формулу (1) в решении задачи 240), находим:

Следовательно, искомое отношение равно