Найти отношение объема правильной n-угольной пирамиды к объему вписанного в нее шара, зная, что окружности, описанные около основания и боковых граней пирамиды, равны между собой.
Пусть а - сторона основания пирамиды, b - апофема основания, R - радиус окружности, описанной около основания, А - высота пирамиды, r - радиус вписанного в пирамиду шара, у - высота боковой грани, проведенная из вершины пирамиды (рис. а и б).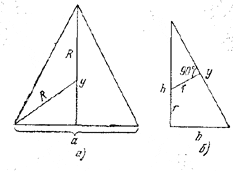
Тогда
a = 2R sin π/n, b = R cos π/n,
кроме того
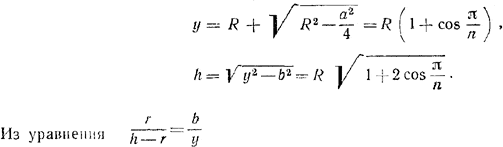
(см. рис. б) находим
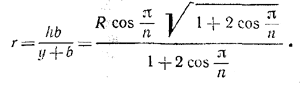
Следовательно, искомое отношение равно
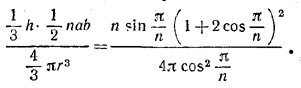
Похожие примеры: