Найти высоту правильной четырехугольной пирамиды, если известно, что объем шара, описанного около пирамиды, равен V, а перпендикуляр, опущенный из центра шара на ее боковую грань, образует с высотой пирамиды угол α.
Пусть а - сторона основания пирамиды SABCD, h - высота пирамиды, r - радиус шара, описанного около пирамиды.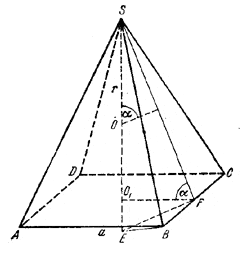
Тогда
V = 4/3 πr3
и
r = (3V/4π) 1/3
Если SE - диаметр описанного шара, то из прямоугольного треугольника SBE следует:
![]()
Так как, однако, из треугольника FO1S имеем a/2 = h ctg α, то, исключая а, находим:
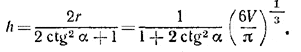
Похожие примеры: