Шар радиуса R вписан в пирамиду, в основании которой лежит ромб с острым углом α. Боковые грани пирамиды наклонены к плоскости основания под углом ψ. Найти объем пирамиды.
Используя равенство двугранных углов, как и в задаче 232 нетрудно показать, что перпендикуляр, опущенный из вершины на основание, проектируется в центр симметрии ромба. Легко также видеть, что центр вписанного шара лежит на указанном перпендикуляре.Пусть а - сторона ромба, 2h - высота ромба, H - высота пирамиды.
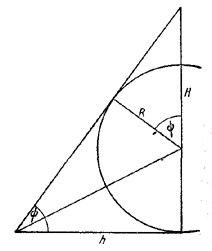
Тогда площадь основания S =a2 sin α или, так как ![]()
![]()
Но h= R ctg ψ/2 (см. рис., где изображено сечение, проходящее через высоту пирамиды и высоту ромба). Ясно также, что
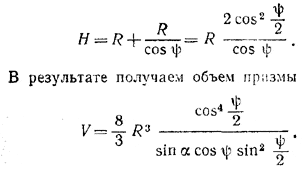
Похожие примеры: