Две правильные n-угольные пирамиды с одинаковыми основаниями сложены этими основаниями. Найти радиус шара, вписанного внутрь получившегося многогранника, зная, что сторона общего основания пирамид равна а, а высоты пирамид равны h и H.
Проведем плоскость через вершины S1 и S2 пирамид и середину А одной из сторон основания.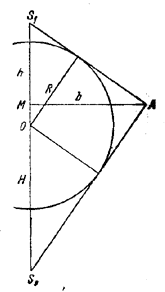
Радиус полукруга, вписанного в треугольник AS1S2 так, что его диаметр лежит на S1S2 очевидно, равен радиусу вписанного шара. Пусть О - центр полукруга. Обозначим через b высоту в треугольнике AS1S2, опущенную на сторону S1S2. Так как b есть апофема правильного n-угольника, то
b = a/2 ctg π/n
Радиус шара R найдем, подсчитав двумя способами площадь S треугольника AS1S2. С одной стороны,
S = b/2(H + h),
с другой стороны,
![]()
В итоге получаем окончательную формулу
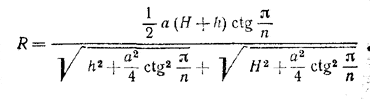
Похожие примеры: