Около шара радиуса r описана правильная n-угольная пирамида, у которой двугранный угол при основании равен α. Найти отношение объема шара к объему пирамиды.
Пусть а - сторона и b - апофема правильного n-угольника, лежащего в основании пирамиды, Н-высота пирамиды. Тогда (рис. а и б)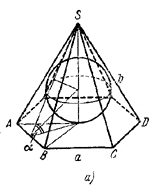
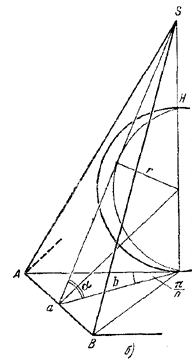
b = r ctg α/2
a = 2b tg π/n= 2r ctg α/2 tg π/n;
площадь основания равна
Sосн. = n ab/2= nr2tg π/nctg2 α/2.
Далее, H = btg α= r tg α ctg α/2. Отсюда объем пирамиды
Vпир.= 1/3 nr3ctg3 α/2 tg α tg π/n
Так как объем шара Vш. = 4/3 πr3, то
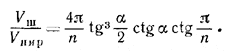
Похожие примеры: