В правильную треугольную пирамиду вписан шар. Определить угол наклона боковой грани пирамиды к плоскости основания, зная, что отношение объема пирамиды к объему шара равно 27√3 /4π.
Обозначим через r радиус вписанного шара ичерез а длину отрезка ОЕ.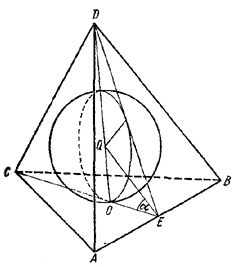
Тогда
r = а tg α,
где α - половина искомого угла. Следовательно, объем шара равен
Vш. = 4/3πа3 tg3 α
Так как DO = а tg 2α, a AB = 2√3 а, то объем пирамиды будет
Vпир.= 1/3DO√3/4 AB2 = √3 а3 tg2α.
Так как по условию задачи
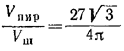
то, выражая tg 2α через tg α, получаем уравнение
tg2 α( 1 - tg2 α) = 2/9
Отсюда (tg α)12 = 1/3 и (tg α)22 = 2/3 .
Учитывая, что α - острый угол, находим:
α1= π/6
и
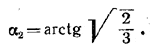
Похожие примеры: