Пусть R - радиус шара, описанного около правильной четырехугольной пирамиды, r- радиус шара, вписанного в эту пирамиду. Доказать, что

^R/_r > √2 + 1
Указание. Выразить ^R/_rчерез tg ^α/₂, где α - двугранный угол между основанием и боковой гранью.

Пусть a - сторона основания данной пирамиды SABCD, α - двугранный угол между боковой гранью и основанием, Н - высота SO - пирамиды.

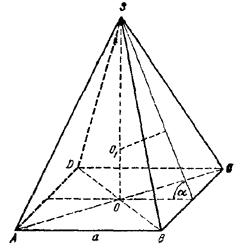
Тогда

r = ^a/₂ tg ^α/₂

Кроме того (см. формулу (1) в решении задачи 254),

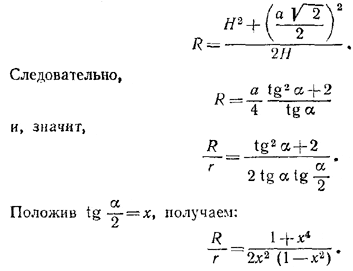
Полагая еще x² = t, мы сведем задачу к доказательству неравенства

при 0 < t < 1.

Умножив на знаменатель обе части неравенства и раскрыв скобки, приходим к неравенству

(2√2 + 3)t² - 2 (√2+1)t + 1 > 0

для квадратного трехчлена. Вычисляя дискриминант трехчлена, обнаруживаем, что он равен нулю. Следовательно, трехчлен не изменяет знака вообще при любых значениях t. Так как при t = 0 он положителен, то неравенство доказано.