Доказать, что при соединении трех вершин правильного тетраэдра с серединой высоты, опущенной из четвертой вершины, получаются три попарно перпендикулярные прямые.

Пусть SD - высота пирамиды SABC, О - середина высоты, Е - середина отрезка ВС, длину которого мы обозначим через a.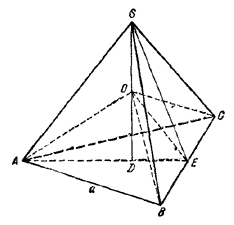

Имеем:

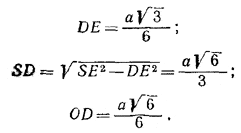
Отсюда

OE = √OD² + DE² = ^α/₂.

Следовательно, ОЕ = ВЕ = ЕС и, значит, ∠ВОС = 90°