Дан усеченный конус, у которого высота есть среднее пропорциональное между диаметрами оснований. Доказать, что в конус можно вписать шар.

Рассмотрим трапецию ABCD, получающуюся в осевом сечении конуса (см. рис.);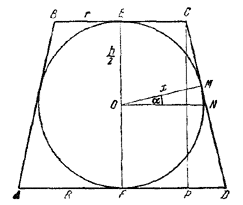

пусть Е и F-середины ее оснований О - середина EF.

ОМ ⊥CD, ON ⊥EF, СР ⊥ AD, ∠MON = ∠PCD = α.

Для решения задачи достаточно показать, что ОМ = ОЕ. Введем обозначения:

EC = r, DF = R, OМ = х, ОE = ^h/₂.

Тогда

Из треугольника CPD имеем:

h = CD cos α = √(R- r)² + СР² cos α

Но так как по условию CP² = 4Rr, то

h = √(R- r)² + 4Rr cos α = (R + r) cos α.

Таким образом, х = ^h/₂, что и требовалось доказать.