Дан усеченный конус, боковая поверхность которого равна площади круга, имеющего своим радиусом образующую усеченного конуса. Доказать, что в данный конус можно вписать шар.

Пусть Е и F - середины оснований трапеции ABCD, полученной в осевом сечении конуса.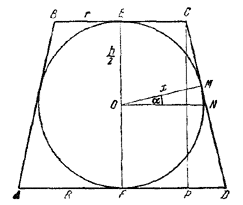

Проведем через середину О отрезка EF прямые ОМ ⊥CD, ON ⊥EF, СР ⊥ AD. Положим для сокращения письма СD = l, EF = h, 0M = x, EC = r, DF = R, ∠MON = ∠PCD = α.

Для доказательства достаточно установить, что х = ^h/₂ Пo

условию πl (R + r) = πl² и, следовательно, R+ r = l. Так как, однако, из треугольников OMN и CPD имеем:

то х = ^h/₂, что и требовалось доказать*).

*) Из полученного выше равенства R+ r = l следует, что 2R + 2r = l + l. Это означает, что суммы противоположных сторон рассматриваемого четырехугольника равны. Последнее уже достаточно для того, чтобы в четырехугольник можно было вписать окружность. Мы, однако, не опираемся на этот факт.